Complex Drags
In this example, a complex drag is executed. Three different nodes have been selected, and both the option key ("take children") as well as the control key ("take parents") were depressed.
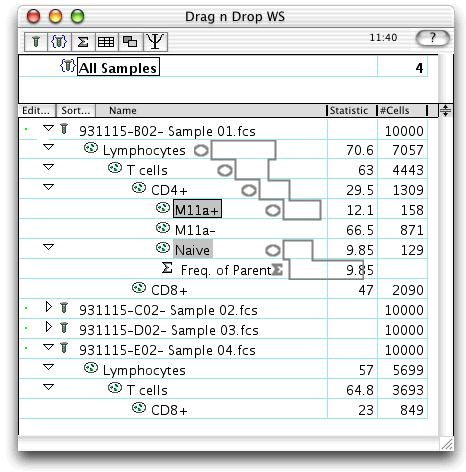
The first graphic shows what the screen looks like when the drag has begun. Note the dotted outline which identifies the nodes being dragged. Since "take parents" was selected, all nodes up to the CD3+ gate are chosen; since "take children" was selected, all of the children of "CD4+" are taken (the other two nodes have no children). Since these multiple nodes have a common ancestor ("CD3+"), you can think of this as taking a single analysis tree based at "CD3+", but only take a subset of its children.
 �
�
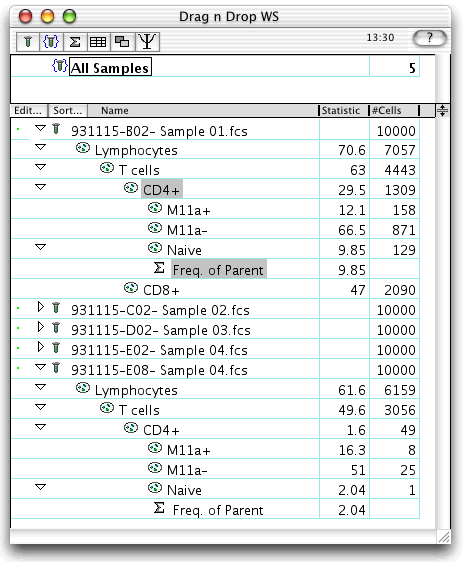
The second graphic shows what happens at the end of the drag.
 �
�
The desired subset of nodes is applied to the destination sample E01: Pt:E(PMA). In general, when you select "take parents", you will drop onto a sample node rather than a subpopulation node, since the original top gate was applied to a sample as well. However, you could drop the tree onto a subpopulation node. For instance, had you created a "Live gate" node on the sample to exclude dead cells, you would have dropped the tree onto this gate so that the new tree is a child of "Live gate".
Go back to the summary of drag and drop examples.
