Change Graph and Models for Cell Cycle Platform
Open the disclosure triangles at the bottom of the Cell Cycle platform window. You can choose the model you wish to apply, change any of the fitting criteria with the click of a button, apply them immediately, and continue to change them until you have satisfactorily fit the data.
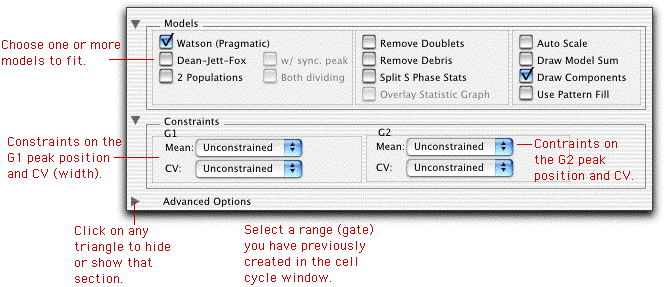
There are three principal models that FlowJo can (simultaneously) compute for any given distribution. These include the "Watson Pragmatic" model, the "Dean-Jett-Fox" model, and the "2-populations" model. The 2-populations model is based on the "Dean-Jett-Fox" model, but simultaneously fits two different dividing populations, each with a single Dean-Jett-Fox model.
The Watson model makes no assumptions about the shape of the S-Phase distribution; it (by definition) fits the S-phase exactly. The DJF model assumes that the S-phase is can be modeled by a second degree polynomial (that is convoluted with gaussian distributions of varying width throughout S-phase). You can also choose to have a synchronized peak within the S-phase as an option to this model.
Once you select one or more models and apply them, you can also choose to constrain the fits. Each gaussian peak (G1, G2, or the synchronous population) can be constrained by absolute position within a defined range (that you have created in the Graph Window), or by relative position to the other peak. For example, if the G2 peak position is twice the intensity of the G1 peak position, you may wish to constrain the fit such that this is always true. This is useful if the G2 peak is difficult to ascertain.
In addition, you can constrain the widths (CV) of each of the Gaussians. Again, you can constrain them either to an absolute value, or you can set one equal to the other. If your G2 peak is difficult to ascertain, you might want to make the assumption that the G1 CV and the G2 CV are equal, and therefore constrain the G2 CV to be equal to the G1 CV.
More hints on fitting the data can be found on the next page.
